Liceo de Niñas Marta Brunet
Departamento de Matemática
RCD/
Guía N º 2
Observación : Desarrolla esta Guía siempre y cuando hayas desarrollado la Guía N º 1 , la que vimos la clase pasada y que lleva por nombre: "Elementos de la Circunferencia".
En esta Guía Aprenderás:
Concepto de ángulo
Angulos inscritos, de centro y semiinscrito en la circunferencia.
Teoremas para calcular diversas medidas de ángulos.
Medición de los arcos
Angulos interiores y exteriores de una circunferencia.
Aplicarás los conceptos aprendidos en una guía que será evaluada.
Primero que todo, debes saber que es un ángulo y como se denota.
Un ángulo es la intersección de dos rectas o dos cuerdas, cuya intersección se llama vértice.
|
|
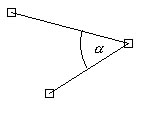
Para denotar un ángulo se usa una letra
griega o un símbolo en la abertura. Aquí en el ejemplo vemos el ángulo
|
|
|
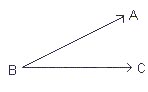
La otra forma de escribir un ángulo es usando tres letras mayúsculas, en el ejemplo el ángulo es ABC donde el vértice corresponde a la letra del medio. |
Ver alfabeto griego Ver actividad Nº 1
¿entendiste? si no has comprendido no sigas avanzando. vuelve a leer y comprender el concepto. ¿o.k?
2.- Ángulos inscritos en la circunferencia:
Se llama ángulo inscrito en una circunferencia a todo ángulo que tiene su vértice sobre la circunferencia y cuyos lados son cuerdas de ella.
Ejemplos de ángulos inscritos:
 |
Al observar bien la figura vemos los
siguientes conceptos:
|
más
ejemplos de ángulos
inscritos:
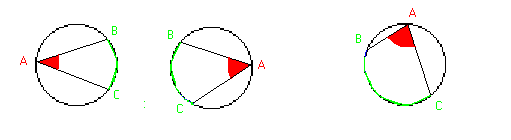
En todos estos ángulos inscritos observamos que
el arco, que abarca el ángulo inscrito, es
¿lo entendiste?. si es efectivo entonces pasa al siguiente concepto.
Se llama ángulo de centro al ángulo que tiene su vértice en el centro de la circunferencia y sus lados son radios de ella.
 |
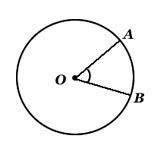Al observar bien la figura vemos los siguientes conceptos:
El ángulo de
centro de la figura es
|
más ejemplos de ángulos de centro:
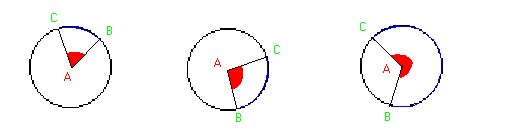
TEOREMA N º 1: Todo ángulo inscrito en una circunferencia es igual a la mitad del ángulo del centro que subtiende el mismo arco.
Observa bien la siguiente figura:
|
|
Todo ángulo inscrito es igual a la mitad del ángulo del centro, siempre y cuando el arco comprendido entre ellos sea común
|
|
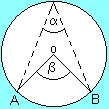
Por ejemplo en la figura ¿cuánto mide ángulo delta? |
 |
Fíjate en la siguiente deducción:
| El
ángulo de centro beta mide el doble de alfa se escribe así: |
 |
¿Quedó claro??
Efectivamente el ángulo de centro es el doble del ángulo inscrito, siempre y cuando subtiendan el mismo arco, es decir, abarca el mismo arco.
|
En la figura ¿cuánto mide el ángulo de centro alfa?
|
|
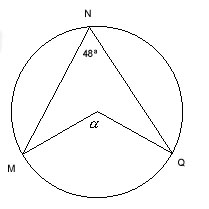
¡Atención!
observa el siguiente ángulo de centro
|
|
Si =62,3º
, entonces el arco AB= 62,3º Por lo tanto : Arco AB =
|
Es decir, todo ángulo de centro tiene la misma medida del arco que lo abarca AB (o subtiende)
Más adelante veremos otra forma de medir arcos. Hasta ahora hemos medidos los arcos sólo en grados sexagesimales.
¡Atención! observa los siguientes ángulos inscritos:
|
|
No importa la ubicación del ángulo inscrito. Todos son iguales si el arco es común.
Observa el arco
¡Todos Iguales! y cada uno mide la mitad del arco AB. Es lo mismo decir que cada uno mide la mitad del ángulo de centro AOB. ¿si?
|
|
|
Los ojos son para mirar ¡úsalos!. ¿Qué nos dice este problema sobre cómo debe entenderse el ángulo del centro correspondiente a un ángulo inscrito? ¿Cuánto mide el ángulo de centro? |
|
|
Cuando el arco AB coincide con el diámetro de la circunferencia, el
ángulo del centro AOB es 180°. Luego el ángulo inscrito es
TEOREMA Nº 2 Teorema de Thales: Todo ángulo inscrito en una semicircunferencia es un ángulo recto. ¡No lo olvides!! |
Veamos un ejemplo:
|
¿Cuánto mide el ángulo x? O centro de la semicircunferencia |
 |
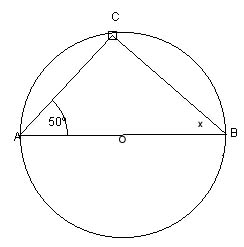No olvides que "la suma de los ángulos interiores de un triángulo es 180º" |
Angulo semiinscrito, es aquel que tiene su vértice en la circunferencia y sus lados son una cuerda y una tangente.
 |
|
|
|
|
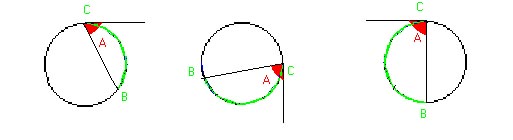TEOREMA N º 3: Su medida también es igual a la mitad del arco que abarca el ángulo A, es decir: |
A= |
 |
Por ejemplo:
En el dibujo, AB es tangente y el arco AC = 120º ¿ Cuál es el valor del ángulo x?
 |
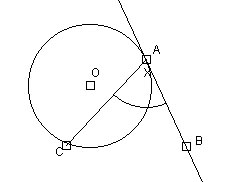Aplicando el Teorema Nº 3 "Todo
ángulo semiinscrito es igual a la mitad de la medida del arco que determina
la cuerda".
Se tiene que el ángulo semiinscrito x es igual a la mitad del arco que lo abarca o subtiende, entonces: si el arco AC = 120 entonces x mide 60º ¿quedó claro?. |
4.- Medición de los arcos:
Los arcos en una circunferencia se leen en el sentido contrario de los punteros del reloj.
|
|
En la figura con rojo se marca el arco AB.
Con azul el arco BA. recuerda en sentido contrario de los punteros del
reloj. ¿Cuánto suman los arcos AB + BA? |
Estudiaremos dos métodos para medir arcos:
A) En grados sexagesimales el arco mide lo mismo que el ángulo del centro que lo subtiende por ejemplo en la siguiente circunferencia el ángulo de centro = medida del arco es decir 96º
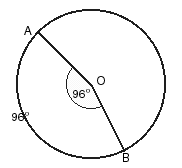Esto
es lo que hemos usado hasta el momento.
B) En Unidades de longitud: podemos concluir que la medida de un arco en grados es directamente proporcional a la medida en cms., por lo tanto si comparamos la medida de un arco con la circunferencia completa obtenemos:
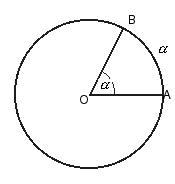
5.-Ángulos Interiores y ángulos exteriores de una circunferencia:
Se llama ángulo interior al ángulo formado por dos cuerdas que se cortan ejemplos:
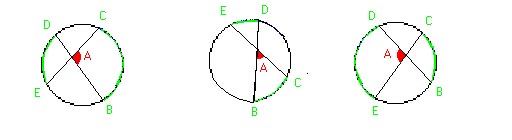
Su medida es igual a la semisuma de los arcos que abarca BC y ED
ángulo exterior es el ángulo formado por dos secantes que tienen un extremo común en el exterior de la circunferencia.
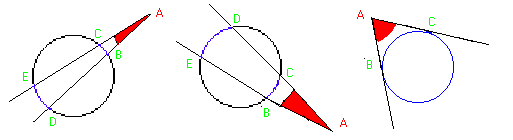
Su medida es igual a la semidiferencia de los arcos que abarca BC y ED
Ahora que has aprendido varios conceptos te invito a desarrollar una guía con ejercicios.
Suerte y mano a la obra!!!
para reforzar visita el siguiente sitio web: http://www.pntic.mec.es/Descartes/Geometria/Los_angulos_en_la_circunferencia/angulosencircunfe1.htm
y 
AOB
y tiene por medida el arco que lo determina o subtiende
es común para todos los ángulos y su medida es una sola.
